Modelado de superficies con TINs ​

La mayoría de los objetos geográficos de un mapa se encuentran en la superficie de la tierra. Entidades como los edificios, las carreteras y los pozos suelen modelarse como entidades -formas vectoriales bidimensionales con atributos, relaciones y comportamiento en conjuntos de datos de características dentro de una base de datos geográfica.

Otras entidades, como los drenajes, las crestas y los picos, son componentes integrales de una superficie. Estas entidades se pueden representar como entidades: sus formas se pueden dibujar claramente en un mapa. Pero si se desea realizar algún tipo de análisis de superficie, como la hidrografía o los estudios de vistas, se debe incluir estas entidades discretas dentro de una representación continua de una superficie.

En capítulos anteriores se analizó el uso versátil de los conjuntos de datos ráster para representar una amplia gama de fenómenos, incluidas las superficies. En este capítulo se compara primero la utilidad de los rásteres y las redes irregulares trianguladas (TIN) para el modelado de superficies, y luego se examina más a fondo la representación de datos TIN.

Características de las superficies ​

Las superficies representan un campo continuo de valores z con un número infinito de puntos. Las computadoras y la noción de infinito son generalmente incompatibles: es necesario algún tipo de muestreo para obtener una aproximación aceptable de una superficie en un SIG.

Los SIGs utilizan dos representaciones para modelar las superficies: los rasters y los TIN. Los rasters representan una superficie como una cuadrícula regular de ubicaciones con valores z muestreados o interpolados. Los TINs representan una superficie como un conjunto de puntos situados irregularmente que forman una red de triángulos con valores z en cada nodo.

Tanto las representaciones ráster como las TIN tienen mérito para el modelado de superficies; el contexto de los datos fuente disponibles, y el alcance del análisis y la cartografía que se debe apoyar, guiarán qué representación es mejor para una aplicación particular.

La representación ráster de una superficie ​

Los rásteres representan las superficies como una cuadrícula regular de ubicaciones uniformemente espaciadas con valores z. Se puede estimar un valor de la superficie para cualquier ubicación interpolando los valores z entre los puntos inmediatos de la cuadrícula.

La resolución de la cuadrícula -la anchura y la altura de las celdas- determina la precisión de la representación raster.

Los rásteres son la representación más común de las superficies porque los datos de elevación están ampliamente disponibles en esta forma a bajo coste. Un ejemplo de datos de superficie rasterizados son los modelos digitales de elevación (DEM) producidos por el Servicio Geológico de Estados Unidos.

Los rásteres admiten un rico conjunto de análisis espaciales, como la coincidencia espacial, la proximidad, la dispersión y las rutas de menor coste, que pueden realizarse rápidamente.

Las desventajas de la representación ráster son que las discontinuidades de la superficie, como las crestas, no están bien representadas y que las ubicaciones precisas de características como los picos se pierden en el muestreo de cuadrícula de los rásters.

Los rásteres son apropiados para aplicaciones cartográficas a pequeña escala en las que la precisión de la posición no es primordial y en las que no es necesario caracterizar con exactitud las características de la superficie.

La representación TIN de una superficie ​

Los TINs representan las superficies como caras triangulares contiguas no superpuestas. Se puede estimar un valor de superficie para cualquier ubicación mediante la interpolación simple o polinómica de las elevaciones en un triángulo.

Dado que las elevaciones se muestrean de forma irregular en un TIN, se puede aplicar una densidad de puntos variable a las zonas en las que el terreno cambia bruscamente, lo que permite obtener un modelo de superficie eficaz y preciso.

Un TIN conserva la ubicación y la forma precisa de las características de la superficie. Las elementos tipo área, como los lagos y las islas, se representan mediante un conjunto cerrado de bordes triangulares. Los elementos lineales, como las crestas, se representan mediante un conjunto conectado de aristas triangulares. Los picos de las montañas se representan mediante un nodo triangular.

Los TIN admiten diversos análisis de superficies, como el cálculo de la elevación, la pendiente y el aspecto, la realización de cálculos de volumen y la creación de perfiles en alineaciones. La desventaja de los TIN es que a menudo no son fáciles de obtener y requieren la recopilación de datos.

Los TIN son muy adecuados para aplicaciones cartográficas a gran escala en las que la precisión posicional y las formas de las características de la superficie son importantes.

Estructura de una TIN ​

La estructura de datos TIN permite representar con precisión cualquier tipo de superficie. No sólo se pueden interpolar las elevaciones de cualquier lugar dentro de un TIN, sino que también se pueden almacenar las características naturales que forman interrupciones en la pendiente de una superficie, como crestas y arroyos.

• El término red irregular triangulada es una descripción concisa de las características de una TIN. "Triangulado" se refiere a la formación de un conjunto optimizado de triángulos a partir de un conjunto de puntos. Los triángulos constituyen una buena representación de una porción local de una superficie porque tres puntos con valores z definen de forma única un plano en el espacio tridimensional.

• "Irregular" identifica la ventaja clave de las TIN para el modelado de superficies: los puntos pueden ser muestreados con una densidad variable para modelar áreas donde el cambio en el relieve de la superficie es abrupto.

• "Red" refleja la estructura topológica implícita en un TIN. Esta estructura permite un análisis sofisticado de la superficie, así como una representación compacta de la misma.

Creación de TINs ​

Los TIN se crean a partir de puntos de masa (hitos), que son puntos con elevaciones recogidas de diversas fuentes. Los TIN se suelen compilar con instrumentos fotogramétricos que toman muestras de elevaciones de pares de fotografías aéreas alineadas con precisión en un modelo estereoscópico. Los TINs también se producen a partir de datos topográficos, curvas de nivel digitalizadas, rasters con valores z, conjuntos de puntos en archivos o bases de datos, u operaciones sobre otros TINs.

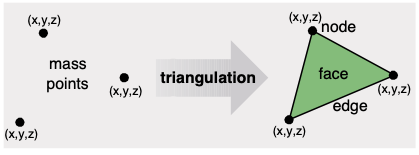
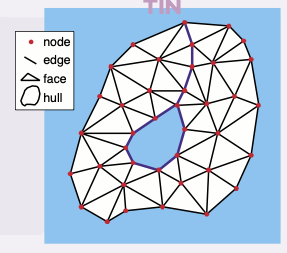
A partir de estos puntos de entrada, se realiza una triangulación en el conjunto de puntos. En un TIN, los triángulos se denominan caras, los puntos se convierten en nodos de una cara, y las líneas de las caras se llaman aristas.

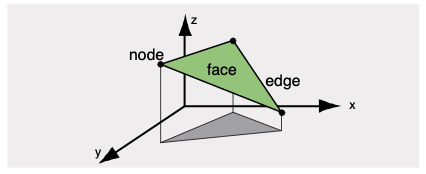
Triangulación y topología ​

Dado un conjunto de puntos, se pueden crear muchas triangulaciones posibles. Los SIGs utilizan un algoritmo llamado triangulación de Delaunay para optimizar la forma en que las caras modelan una superficie.

La idea básica de este algoritmo es crear triángulos que colectivamente sean lo más parecido a formas equiláteras. Esto mantiene la interpolación de las elevaciones en los nuevos puntos más cerca de los puntos de entrada conocidos.

Se puede realizar una triangulación a partir de un conjunto de características de superficie representadas por puntos, líneas y áreas. En primer lugar, se realiza una triangulación a partir de puntos. A continuación, se insertan líneas en la triangulación y se crean nuevos nodos allí donde esas líneas dividen caras. Por último, se insertan áreas, que también pueden dividir o recortar caras.

Una vez completada la triangulación, el TIN almacena una lista de nodos para cada cara, y para cada cara, una lista de caras vecinas. Esta representación es similar a la topología representada por las topologías planas. La diferencia es que los nodos tienen elevaciones y las caras deben ser triángulos en lugar de polígonos arbitrarios.

Modelado de los elementos de la superficie ​

Se puede crear un TIN introduciendo elementos de la superficie que representen características del terreno como elevaciones de puntos, picos, arroyos y crestas.

Las elevaciones de puntos son la entrada predominante en un TIN y forman la forma general de la superficie. Pueden introducirse a partir de curvas de nivel si es necesario, pero es mejor utilizar puntos recogidos con dispositivos fotogramétricos porque el operador puede hacer un mejor trabajo de muestreo visual de los puntos que reflejan el relieve del terreno.

A continuación, se añaden los arroyos, las crestas y otras características superficiales similares para perfeccionar el modelo de superficie y afinar los cambios de relieve. Estas características se conservan en el TIN y aumentan la precisión del modelo.

Representación de la morfología del terreno ​

La morfología del terreno es una representación de las características de la superficie tal y como se muestra en muchos mapas. Estas características pueden convertirse en un TIN.

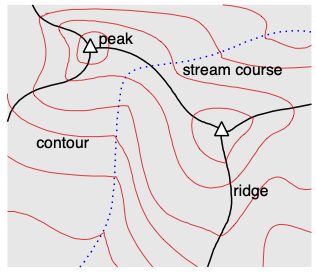
Elementos puntuales ​

Los puntos de masa (hitos) representan puntos en los que se mide un valor z. Tras la triangulación, se conservan como nodos con la misma ubicación y elevación.

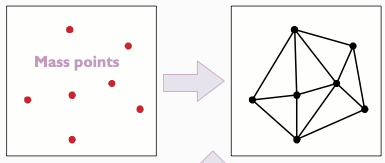
Elementos lineales ​

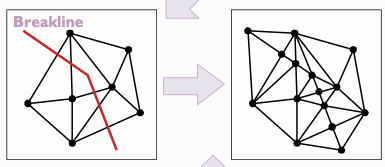
Las líneas de ruptura son características lineales que representan rasgos naturales, como cursos y crestas, o rasgos artificiales, como carreteras. Hay dos tipos de líneas de ruptura: duras y blandas.

Las líneas de rotura duras representan una discontinuidad de la pendiente, como el curso de un arroyo. Aunque la superficie es siempre continua, su pendiente puede no serlo. Las líneas de rotura duras conservan la nitidez de la superficie y mejoran el análisis y la visualización de un TIN.

Las líneas de rotura suaves permiten añadir bordes para representar características lineales, pero no representan una discontinuidad de pendiente. Por ejemplo, es posible que se desee añadir la huella de una carretera a un modelo de superficie, pero sin alterar significativamente la pendiente local de la superficie.

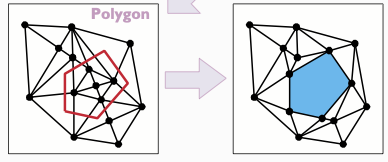
Elementos poligonales ​

Los polígonos representan objetos como lagos o costas. Borrar polígonos marca todas las áreas dentro del polígono como fuera de la zona de interpolación. Las operaciones analíticas como los cálculos de volumen, el contorno y la interpolación ignorarán estas áreas.

• Los polígonos de reemplazo asignan un valor z constante al límite y a todas las alturas interiores.

• Los polígonos de recorte marcan todas las áreas fuera del polígono como si estuvieran fuera de la zona de interpolación para el modelo.

• Los polígonos de relleno asignan un valor de un atributo entero a todas las caras dentro del polígono. No se produce ninguna sustitución de altura, borrado o recorte.

Superficies funcionales ​

Un TIN es una representación de una superficie con un valor z único para cada punto. Una cualidad interesante de la representación de datos TIN es que representa puntos en un espacio tridimensional, pero la red topológica de caras está limitada a dos dimensiones.

Por esta razón, a veces se dice que la representación de datos TIN modela "dos dimensiones y media". Esta descripción no es del todo exacta, pero ilustra el hecho de que las superficies tienen puntos medidos en tres dimensiones, pero cada punto sólo puede tener un valor z.

Por lo tanto, las TIN son un ejemplo de función de valor único: dada una ubicación de entrada, sólo se puede interpolar un valor z. Una pequeña limitación de los TIN es que no pueden modelar los casos poco frecuentes de pendiente negativa, como los acantilados y las cuevas que sobresalen.

Ejercicios ​

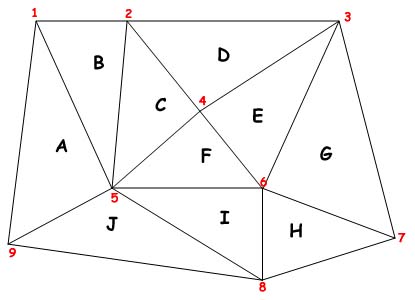
12.1. A partir de los puntos que se muestran más abajo dibuje una posible Red Triangular Irregular (TIN). Además calcule la elevación para el centroide de cada triángulo generado.

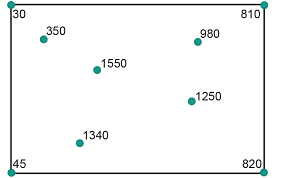
12.2. Dada la TIN que se muestra más abajo, muestre la tabla de triángulos asociada junto con la lista de nodos y vecinos.