Análisis de datos puntuales ​

Las herramientas de interpolación de superficies crean una superficie continua (o de predicción) a partir de valores puntuales muestreados.

Visitar todos los lugares de un área de estudio para medir la altura, la concentración o la magnitud de un fenómeno suele ser difícil o caro. En su lugar, se puede medir el fenómeno en lugares de muestreo estratégicamente dispersos, y los valores predichos se pueden asignar a todos los demás lugares. Los puntos de entrada pueden estar espaciados de forma aleatoria o regular o basarse en un esquema de muestreo.

La representación de la superficie continua de un conjunto de datos ráster representa alguna medida, como la altura, la concentración o la magnitud (por ejemplo, la elevación, la acidez o el nivel de ruido). Las herramientas de interpolación de superficies realizan predicciones a partir de las mediciones de las muestras para todas las ubicaciones de un conjunto de datos ráster de salida, se haya realizado o no una medición en la ubicación.

Hay varias formas de obtener una predicción para cada lugar; cada método se denomina modelo. Con cada modelo, se hacen diferentes suposiciones de los datos, y ciertos modelos son más aplicables para datos específicos; por ejemplo, un modelo puede tener en cuenta la variación local mejor que otro. Cada modelo produce predicciones utilizando diferentes cálculos.

Interpolación ​

Interpolación es el procedimiento de predecir el valor de los atributos en sitios no muestreados desde medidas hechas en localizaciones puntuales dentro de una misma área o región. Predecir el valor de un atributo en sitios fuera del área cubierta por observaciones existentes es llamado extrapolación.

La interpolación es usada para convertir datos desde observaciones puntuales a superficies continuas, de forma que los patrones espaciales muestreados por estas mediciones, puedan ser comparados con patrones espaciales de otras entidades espaciales. La interpolación es necesaria cuando:

• La superficie discretizada tiene un diferente nivel de resolución, tamaño de celda u orientación a la requerida. Por ejemplo, cuando se realiza la conversión de imágenes rastreadas (documentos, fotografía aérea, o imágenes de satélite) con un tamaño y/o orientación a otra. Este procedimiento se conoce como convolución.

• Una superficie continua es representada por un modelo de datos que es diferente del requerido. Por ejemplo, cuando se requiere la transformación de una superficie continua a otro tipo de representación: de TIN a raster, de raster a TIN, o de vector a raster.

• Los datos no cubren completamente el área de interés. Un ejemplo de ello es la conversión de datos desde conjuntos de puntos muestreados a superficies continuas.

La hipótesis que hace que la interpolación sea una opción viable es que los objetos distribuidos espacialmente están correlacionados espacialmente; en otras palabras, las cosas que están cerca tienden a tener características similares. Por ejemplo, si está lloviendo en un lado de la calle, se puede predecir con un alto nivel de confianza que está lloviendo en el otro lado de la calle. No se estaría tan seguro si lloviera al otro lado de la ciudad y menos aún sobre el estado del tiempo en el siguiente condado.

Utilizando la analogía anterior, es fácil ver que los valores de los puntos cercanos a los puntos muestreados tienen más probabilidades de ser similares que los que están más alejados. Esta es la base de la interpolación. Un uso típico de la interpolación de puntos es crear una superficie de elevación a partir de un conjunto de mediciones de muestra.

Muestreos puntuales ​

El diseño del muestreo es una parte fundamental de cualquier estudio que implique la elaboración de modelos y estimaciones a partir de datos muestreados de los recursos naturales u otros fenómenos que ocurren en el paisaje. Las consideraciones estadísticas relacionadas con el muestreo forman parte de un escenario más amplio en el que intervienen los conocimientos teóricos, el comportamiento y los patrones del fenómeno detectados previamente, los costes, la accesibilidad a los lugares de muestreo, la política, etc. Por lo tanto, el algoritmo de diseño del muestreo debe ser lo suficientemente flexible como para dar cabida a consideraciones externas en el diseño.

Actualmente, se ofrecen algunos métodos para construir diseños de muestreo:

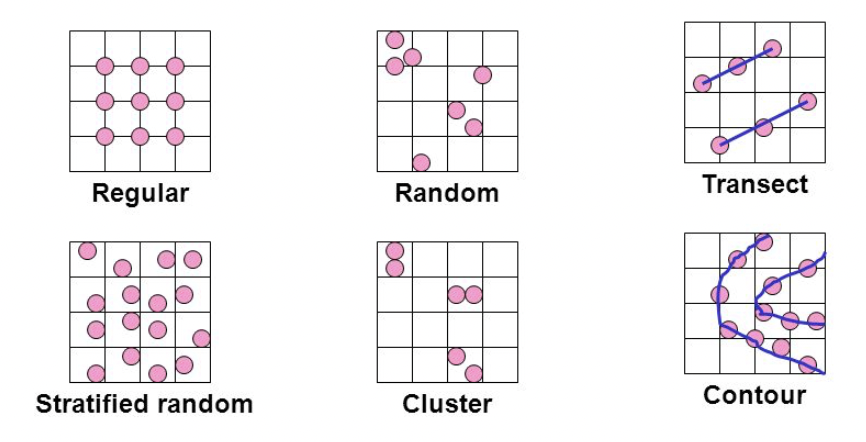
• Muestreo regular: Un muestreo completamente regular puede ser factible. Sin embargo, el muestreo puede coincidir con la distribución espacial de los fenómenos geográficos. Por ejemplo: drenajes espaciados o árboles.

• Muestreo aleatorio simple: Los sitios se muestrean de forma independiente. El método es sencillo y flexible, pero el resultado de un estudio puede incluir zonas en las que las muestras están agrupadas y otras zonas que carecen de ellas.

• Muestreo aleatorio estratificado: El área de estudio se divide en estratos y se obtienen muestras aleatorias dentro de cada estrato. Los estratos pueden ajustarse basándose en el conocimiento previo del fenómeno (por ejemplo, los círculos concéntricos pueden hacerse más grandes a medida que aumenta la distancia de una fuente de emisión puntual), proporcionando cierta estructura espacial a la muestra.

Otros tipos de diseños pueden generarse con relativa facilidad utilizando modelos sencillos:

• Muestreo aleatorio sistemático: Se elige al azar un lugar de la muestra inicial y todos los demás lugares se seleccionan de forma que estén situados según algún patrón regular (por ejemplo, en los vértices de triángulos equiláteros, cuadrados, hexágonos, etc.). El método es sencillo y proporciona diseños espacialmente bien equilibrados (bien distribuidos en el espacio).

• Muestreo aleatorio agrupado: La ubicación de un grupo de emplazamientos se selecciona al azar, y los emplazamientos dentro de cada grupo se ubican relativamente cerca unos de otros. Este método es fácil de aplicar en la práctica, ya que muchas muestras se recogen en lugares cercanos (a diferencia de un patrón de muestreo aleatorio simple, en el que los lugares de muestreo pueden estar en cualquier parte del área de estudio).

Estos métodos no tienen en cuenta las variaciones en la probabilidad de que un lugar sea seleccionado (aparte de dividir el área de estudio en estratos, lo que suele requerir una inspección manual del lugar de estudio y un buen conocimiento del proceso estudiado). Además, no todos ellos garantizan que el diseño de muestreo sea espacialmente equilibrado (es decir, que el diseño muestre a toda la población, debido a la aleatoriedad inherente a la selección de un sitio para el muestreo).

Superficie de tendencia ​

La superficie de tendencia utiliza una interpolación polinómica global que ajusta una superficie suave definida por una función matemática (un polinomio) a los puntos de muestra de entrada. La superficie de la tendencia cambia gradualmente y captura los patrones de escala gruesa en los datos.

Conceptualmente, la interpolación de tendencias es como tomar un trozo de papel y ajustarlo entre puntos elevados (elevados a la altura del valor). Esto se demuestra en el siguiente diagrama para un conjunto de puntos de muestra de elevación tomados en una colina de suave pendiente.

Un trozo de papel plano no capturará con precisión un paisaje que contenga un valle. Sin embargo, si se dobla el trozo de papel una vez, se obtiene un mejor ajuste. Si se añade un término a la fórmula matemática, se obtiene un resultado similar, un doblez en el plano. Un plano (sin doblar el papel) es un polinomio de primer orden (lineal). Si se permite un pliegue, se obtiene un polinomio de segundo orden (cuadrático), dos pliegues de tercer orden (cúbico), y así sucesivamente.

Rara vez el trozo de papel pasará por los puntos medidos reales, lo que hace que la interpolación de la tendencia sea un interpolador inexacto. Algunos puntos estarán por encima del trozo de papel y otros por debajo. Sin embargo, si se suma cuánto más alto está cada punto por encima del trozo de papel y se suma cuánto más bajo está cada punto por debajo del trozo de papel, las dos sumas deberían ser similares. La superficie, se obtiene mediante un ajuste de regresión por mínimos cuadrados. La superficie resultante minimiza las diferencias al cuadrado entre los valores elevados y la hoja de papel.

Cuanto menor sea el error cuadrático medio (RMS), más fielmente representará la superficie interpolada los puntos de entrada. Los órdenes más comunes de los polinomios son del uno al tres. La interpolación de superficies de tendencia crea superficies suaves.

Cuándo utilizar la interpolación de tendencia ​

La interpolación de tendencias da lugar a una superficie suave que representa las tendencias graduales de la superficie en el área de interés. Este tipo de interpolación puede utilizarse para:

• Ajustar una superficie a los puntos de la muestra cuando la superficie varía gradualmente de una región a otra sobre el área de interés-por ejemplo, la contaminación sobre un área industrial.
• Examinar o eliminar los efectos de las tendencias globales o de largo alcance. En estas circunstancias, la técnica suele denominarse análisis de superficie de tendencia.

Vecinos cercanos (polígonos de Thiessen) ​

El método de vecinos cercanos encuentra el subconjunto de muestras de entrada más cercano a un punto de consulta y les aplica pesos basados en áreas proporcionales para interpolar un valor. También se conoce como interpolación de Sibson o de "robo de área". Sus propiedades básicas son que es local, ya que sólo utiliza un subconjunto de muestras que rodean un punto de consulta, y se garantiza que las alturas interpoladas están dentro del rango de las muestras utilizadas. No infiere tendencias y no producirá picos, pozos, crestas o valles que no estén ya representados por las muestras de entrada. La superficie pasa a través de las muestras de entrada y es suave en todas partes excepto en las ubicaciones de las muestras de entrada.

Los vecinos cercanos de cualquier punto son los asociados a los polígonos de Voronoi (Thiessen) vecinos. Inicialmente, se construye un diagrama de Voronoi con todos los puntos dados. A continuación, se crea un nuevo polígono de Voronoi, alrededor del punto de interpolación. La proporción de solapamiento entre este nuevo polígono y los polígonos iniciales se utiliza entonces como pesos.

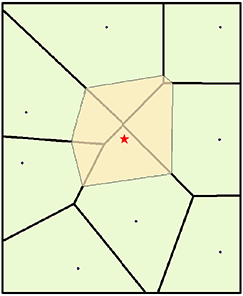
Los polígonos de Thiessen llevan el método de interpolación hasta el extremo ya que la predicción de atributos, en posiciones no muestreadas, es provista por el dato puntual más cercano. Los polígonos de Thiessen dividen la región en una forma que está totalmente determinada por la configuración de los datos puntuales, con una observación por polígono.

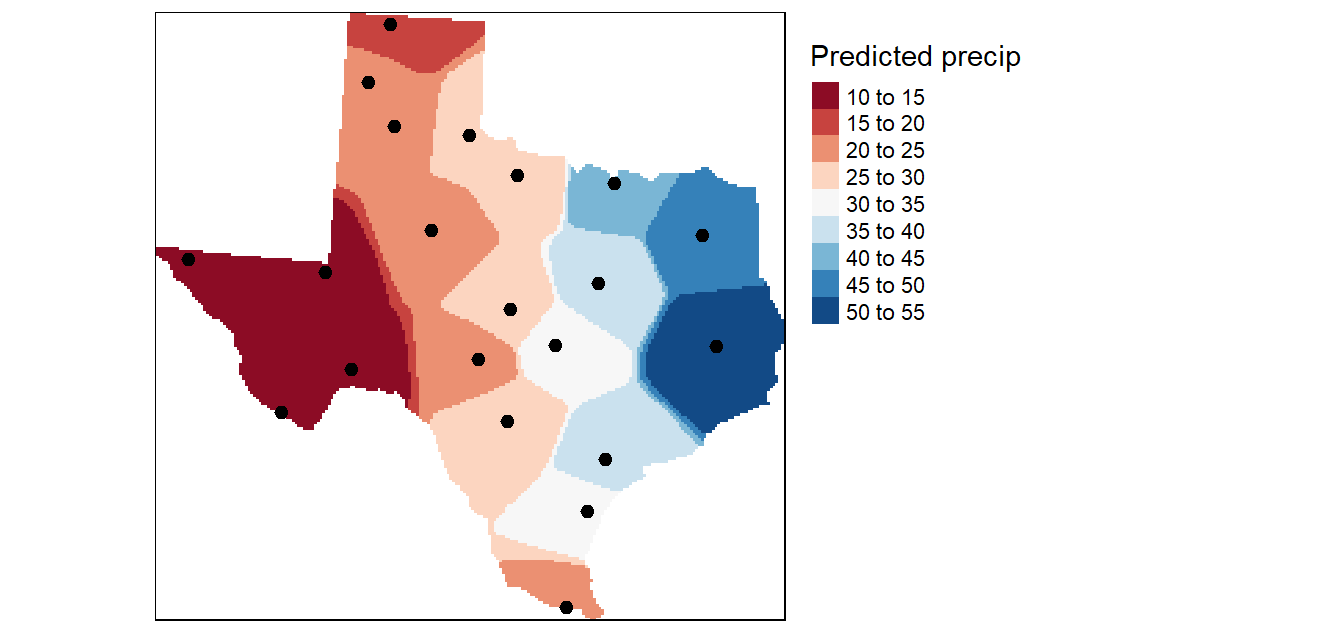
Si los datos siguen una rejilla cuadrada regular, entonces los polígonos de Thiessen son todos celdas regulares de igual tamaño; si los datos están espaciados en forma irregular entonces los polígonos tendrán también una forma irregular. Las líneas que unen los datos puntuales forma la llamada Triangulación de Delaunay, que es la misma topología de un TIN.

Cuándo utilizar vecinos cercanos ​

Una ventaja de los polígonos de Thiessen es que ellos pueden ser fácilmente usados con datos cuantitativos como clases de vegetación o usos de terreno si todo lo que se necesita es un mapa sencillo. Debido a que todas las predicciones igualan a los datos puntuales, los polígonos de Thiessen se consideran un método de predicción exacto.

Distancia inversa ponderada ​

Los métodos de distancia inversa (IDW) combinan las ideas de proximidad, expuestas por los polígonos de Thiessen, y de cambio gradual de las superficies de tendencia. La suposición es que el valor de un atributo Z en algún punto no visitado un promedio ponderado del valor y distancia de los datos puntuales que ocurren dentro de un vecindario o ventana alrededor del punto.

Esta interpolación determina los valores de las celdas mediante una combinación linealmente ponderada de un conjunto de puntos de muestra. El método estima los valores de las celdas promediando los valores de los puntos de datos de muestra en la vecindad de cada celda de procesamiento. Cuanto más cerca esté un punto del centro de la celda que se está estimando, más influencia, o peso, tendrá en el proceso de promediación.

Este método parte de la base de que la influencia de la variable que se está cartografiando disminuye con la distancia a la que se encuentra la muestra. Por ejemplo, al interpolar una superficie de poder adquisitivo de los consumidores para un análisis de un lugar de venta al por menor, el poder adquisitivo de un lugar más lejano tendrá menos influencia porque es más probable que la gente compre más cerca de su casa.

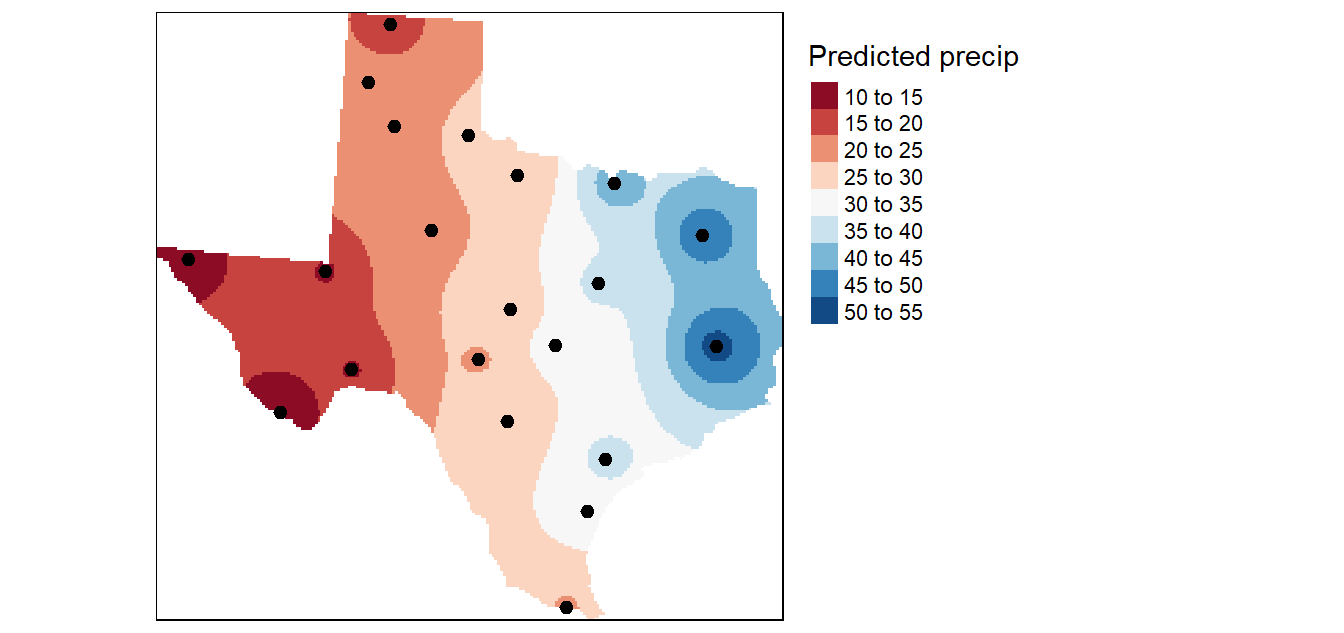
La forma más común de este método es llamada distancia inversa ponderada en la cuál el cálculo de los pesos que tendrán los datos se realiza mediante una función lineal de la distancia entre dicho conjuntos de datos y el punto a ser determinado. Por ejemplo, si una celda cuenta con tres vecinos con valores 2, 4, 5 y a distancias de 2, 3 y 5 respectivamente; entonces los pesos respectivos serían (1/2) / (1/10) = 0.5263, (1/3) / (1/10) = 0.2631 y (1/5) / (1/10) = 0.2105 dando por resultado un valor estimado de 1.0526 + 1.0524 + 1.0525 = 3.1575.

Es importante definir el tamaño del vecindario, si este es grande entonces muchos valores influyen y las variaciones locales se diluyen, y si este es pequeño entonces solo los valores cercanos tendrán algún peso y las variaciones locales adquieren importancia.

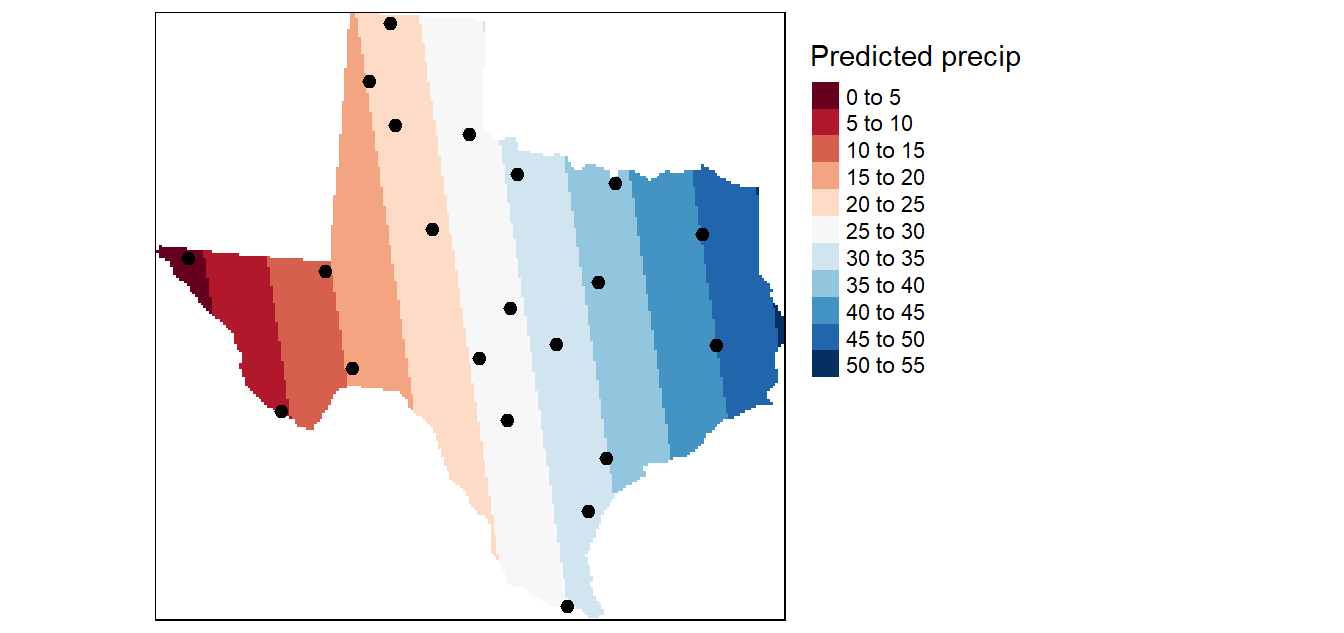
La interpolación por distancia inversa es usada comúnmente en SIGs para crear traslapes raster desde datos puntuales. Una vez que los datos están en una rejilla regular, las líneas de contorno pueden ser obtenidas a través de interpolación de valores y el mapa puede ser dibujado como un mapa de vectores de contorno o como un mapa raster con sombreado.

Limitación de los puntos ​

Las características de la superficie interpolada también pueden controlarse limitando los puntos de entrada utilizados en el cálculo del valor de cada celda de salida. Limitar el número de puntos de entrada considerados puede mejorar la velocidad de procesamiento. También hay que tener en cuenta que los puntos de entrada alejados de la ubicación de la celda en la que se realiza la predicción pueden tener una correlación espacial pobre o nula, por lo que puede haber razones para eliminarlos del cálculo.

Se puede especificar el número de puntos a utilizar directamente, o especificar un radio fijo dentro del cual se incluirán los puntos en la interpolación.

Utilización de barreras ​

Una barrera es un conjunto de datos de polilíneas utilizado como línea de ruptura que limita la búsqueda de puntos de muestra de entrada. Una polilínea puede representar un acantilado, una cresta o cualquier otra interrupción en un paisaje. Sólo se tendrán en cuenta los puntos de muestra de entrada situados en el mismo lado de la barrera que la celda de procesamiento actual.

Método Splines ​

Las curvas splines utilizan un método de interpolación que estima los valores mediante una función matemática que minimiza la curvatura global de la superficie, dando como resultado una superficie suave que pasa exactamente por los puntos de entrada. Este método es mejor para generar superficies que varían suavemente, como la elevación, las alturas de la capa freática o las concentraciones de contaminación.

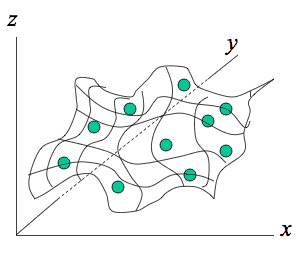
Las curvas splines son funciones en partes, que se ajustan a un pequeño número de datos puntuales en forma exacta, mientras al mismo tiempo aseguran que las uniones entre una parte de la curva y la otra son continuas. A diferencia de una superficie de tendencia, una curva spline pasa exactamente entre los puntos muestreados. Además, con curvas splines es posible modificar una parte de la curva sin tener que recalcularla completa, que no es posible con las superficies de tendencia.

Debido a la dificultad de calcular splines simples sobre un amplio rango de sub-intervalos separados, tal como podría ser el caso de una línea digitalizada, muchas aplicaciones prácticas utilizan un tipo especial de spline llamada B-splines. B-splines son ellas mismas la suma de otras splines que por definición tienen el valor cero fuera del intervalo de interés.

Existen algunas variantes en el método de splinea, entre ellas se encuentra el método de spline regularizado que incorpora la primera derivada, la segunda derivada, y tercera derivada en el cálculo de minimización. El método spline regularizado ponderado es otra variante que crea un spline mas suavizado que cambia gradualmente, con valores que pueden estar fuera del rango de datos de la muestra. Por último, el método de spline con tensión controla la rigidez de la superficie según el carácter del fenómeno modelado y crea una superficie menos suave (aspera) con valores más restringidos por el rango de datos de la muestra.

Ejercicios ​

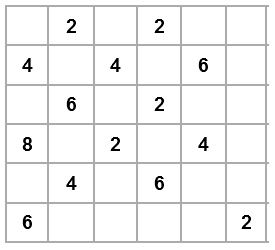
6.1. Muestre el resultado de ejecutar una interpolación espacial sobre la rejilla que se muestra abajo, utilizando los siguientes métodos:

• a. Basada en vecino más cercano (si existen empates, utilice el vecino menor)
• b. Basada en promedios (utilice el vecindario adyacente a cada celda)