Appearance
Análisis de superficies continuas
Una de las mayores ventajas con la representación raster en donde cada atributo es registrado en una capa separada, es que cualquier operación matemática ejecutada en uno o más atributos para la misma celda puede ser aplicada fácilmente a todas las otras celdas que las traslapan. Esto significa que se puede usar exactamente la misma notación algebraica para operar en datos en rejilla como con datos numéricos simples. Este método es llamado Algebra de mapas y el procedimiento de utilizar técnicas algebraicas para construir modelos de análisis espacial es llamado Modelado Cartográfico.
Los métodos del álgebra de mapas significan que el usuario requiere solo especificar las operaciones espaciales a ser usadas y los nombres de las capas fuente y la capa resultante, el programa entonces aplica la operación a todas las celdas en las capas. Esto hace muy fácil escribir modelos de computadora como una secuencia de cálculos, y hace muy fácil la extensión de modelos puntuales formales en el espacio de dos dimensiones.
Operadores del algebra de mapas
Las operaciones de álgebra de mapas son similares a operaciones de traslape, pero cuando se comparan las capas, existe un componente algebraico o matemático.
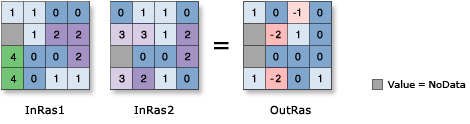
Las operaciones de traslape tienden a usar expresiones que contienen And, Or, y Xor, o conectores booleanos estándar. El álgebra de mapas usa expresiones matemáticas que normalmente retornan valores numéricos. Estos valores son asignados a una rejilla de salida. La siguiente figura muestra el resultado de ejecutar la operación: OutRas = Raster("InRas1") - Raster("InRas2")
Tipos de operadores
Los operadores del álgebra de mapas usualmente ejecutan una acción en dos rejillas de entrada o números. Se pueden distinguir los siguientes tipos de operadores: aritméticos, booleanos, relacionales y a nivel de bits.
Operadores aritméticos
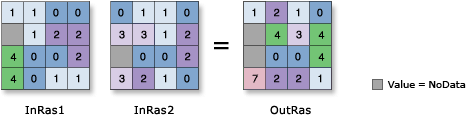
Estos son operadores matemáticos básicos. Incluyen los operadores de: substración, multiplicación, división, potencia y módulo. La siguiente figura muestra el resultado de ejecutar la operación: OutRas = Raster("InRas1") + Raster("InRas2")
Operadores relacionales
Los operadores relacionales comparan dos valores de celdas. Si se cumple la comparación, un 1 es retornado. Sino un cero es retornado. Los operadores relacionales incluyen: menor, menor o igual, diferente, igual, mayor, y mayor o igual. La siguiente figura muestra el resultado de ejecutar la operación: OutRas = Raster("InRas1") == Raster("InRas2")
Operadores booleanos
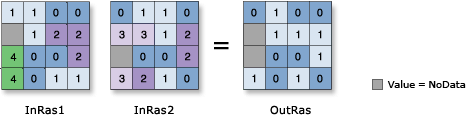
Los operadores booleanos examinan lógicamente la rejilla de entrada. La rejilla de salida contendrá valores de o (falso) y 1 (verdadero). Los operadores booleanos incluyen: AND (y lógico), OR (o lógico), XOR (o exclusivo), y NOT (negación). La siguiente figura muestra el resultado de ejecutar la operación: OutRas = Raster("InRas1") && Raster("InRas2")
Procesamiento condicional
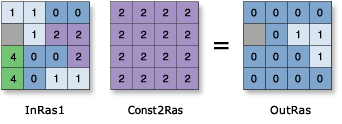
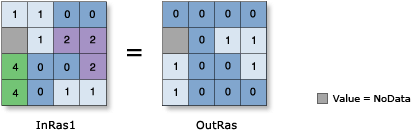
El procesamiento condicional da el poder de controlar el flujo de operaciones. Este permite especificar las condiciones que deben ser evaluadas como verdaderas antes de que una acción sea tomada y especifican las acciones apropiadas para las condiciones falsas. La siguiente figura muestra el resultado de ejecutar la operación: OutRas = Raster("InRas1") >= 2
Funciones del álgebra de mapas
Existen diferentes niveles de funciones del álgebra de mapas categorizados por la celda o celdas consideradas cuando se calcula la salida procesando celda o celdas. La extensión espacial de las celdas de entrada consideradas para la salida podrían incluir una celda, un vecindario de celdas, una zona o región de celdas, o todas las celdas (procesamiento global).
Funciones locales
Las funciones locales ejecutan el procesamiento celda-por-celda. El valor de salida en cada posición depende solo de la celda de entrada en esa posición. Las funciones locales son divididas en seis categorías, que incluyen trigonométricas, exponenciales, logarítmicas, reclasificación, extracción, y estadísticas.
Durante una operación, la función seleccionada procesa la primera celda en la capa de entrada y escribe el resultado a la correspondiente celda en la capa de salida. El procesamiento luego se mueve a la siguiente celda y ejecuta la misma operación, escribiendo los resultados en la rejilla de salida. Si existe más de una capa de entrada, entonces todas las celdas correspondientes a esa misma posición son procesadas.
Existen cuatro subgrupos de funciones matemáticas: logarítmicas, aritméticas, trigonométricas, y potencias. Estas funciones matemáticas son consideradas funciones locales debido a que procesa una celda a la vez.
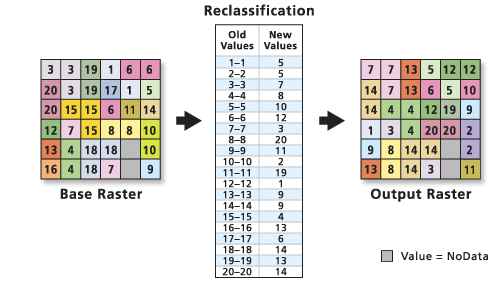
Reclasificación
La función de reclasificación es una técnica de generalización para reasignar valores en un capa de entrada para crear una nueva capa de salida.
Funciones focales y de bloque
Las funciones de bloque y focales ejecutan procesamiento de celdas, pero a diferencia de las funciones locales que son influenciadas por el valor de una única celda, las funciones de bloque y focales consideran los valores de todas las celdas en un vecindario.
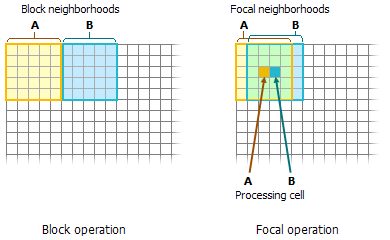
Las funciones de bloque calculan un valor de salida basado en los valores de las celdas de entrada dentro del vecindario. La rejilla de entrada es particionada primero en bloques rectangulares, que no se traslapan, tan grandes como se defina el vecindario. El vecindario es centrado dentro del bloque y los cálculos son ejecutados en las celdas de entrada dentro del vecindario. El resultado es escrito a todas las celdas de salida que se encuentran dentro del bloque. La siguiente figura muestra el resultado de aplicar la siguiente operación: OutRas = BlockStatistics(InRas1, Block(3,3), "MAXIMUM")
Existen dos diferencias entre las funciones de bloque y las funciones focales. Primero, los vecindarios en los bloques no se traslapan, mientras los vecindarios focales siempre se traslapan para procesar cada celda de salida. Segundo, las funciones de bloque calculan un valor y asignan este a todas las celdas en el vecindario, mientras las funciones focales calculan el valor para una celda de procesamiento a la vez.
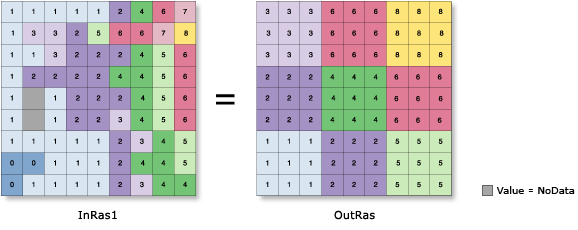
Existen muchas operaciones estadísticas que pueden ser ejecutadas en el vecindario para calcular el valor de la celda o celdas a procesar: media o mediana, mínimo o máximo, mayoría o minoría, rango (mayor menos menor), desviación estándar, suma, variedad, y diversidad (cantidad de valores diferentes). La siguiente figura muestra el resultado de aplicar la siguiente operación: OutRas = FocalStatistics(InRas1, Block(3,3), "SUM")
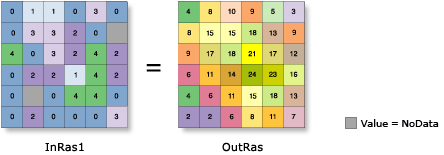
Un ejemplo podría ser examinar un vecindario de vegetación y retornar la diversidad de especias. En un estudio de uso del suelo, se podría determinar cuantos usos diferentes existen en un vecindario definido.
Funciones zonales
El valor de cada celda en la rejilla de salida depende del valor de todas las celdas en la rejilla de entrada que comparten la misma zona. Una zona es un conjunto de posiciones que tienen el mismo valor.
Funciones geométricas zonales
Las funciones geométricas zonales calculan una descripción geométrica para cada zona. El valor geométrico calculado para cada zona (o sea, área) es escrito para todas las celdas en esa zona. Usualmente las zonas son divididas en regiones antes que las medidas sean hechas. A veces es la medida final de conveniencia ( por ejemplo, la zona no debe ser mayor a 40 acres).
Generalmente se calculan cuatro funciones geométricas: el área de la zona, el perímetro de la misma, la delgadez, y el centroide. La delgadez se calcula mediante el círculo de radio máximo que cabe dentro de la zona. El centroide es el punto central de la mayor elipse que cabe dentro de la zona.
La redondez es una medida de la compactitud de un área. Esto es, un círculo es más compacto que un largo lago. Si uno se encuentra en un mall, seguramente prefiere que este sea compacto y no que tenga una figura alargada.
La fórmula de cálculo es: redondez = perímetro/(3.54*área), el valor retornado será 1 para un círculo perfecto y valores mayores para figuras más complejas.
Funciones globales
Las funciones globales calculan una rejilla de salida donde los valores para cada celda es potencialmente una función de todas las celdas de entrada. Muchas de las funciones globales necesitan accesar todas las celdas en la rejilla de entrada para derivar el valor de salida. Las funciones globales son divididas en: agrupamiento de celdas, reclasificación (porciones), distancia euclídea, distancia con pesos, y camino de menor costo.
Agrupamiento de celdas
Las funciones de agrupamiento de celdas crean regiones para una rejilla de entrada. Una región es un grupo de celdas conectadas con el mismo valor. Una zona es un grupo de celdas conectadas o desconectadas con el mismo valor (o sea, todas las celdas en la rejilla con el mismo valor). La función de agrupamiento asigna un valor único a cada región en la rejilla. La siguiente figura el agrupamiento de celdas ortogonal respetando distintos valores:
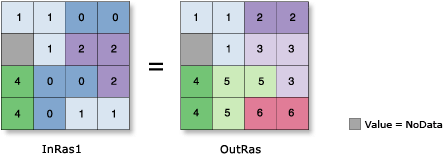
Cuando las celdas son agrupadas juntas, la conectividad de las celdas vecinas es evaluada. Las celdas que están conectadas en diagonal pueden ser consideradas o no.
Se pueden considerar dos formas de agrupamiento. Una forma agrupa celdas sin importar su valor, pero respetando los valores de exclusión; la otra forma agrupa solo aquellas celdas con el mismo valor de entrada.
Los valores de exclusión especifican el valor de la(s) zona(s) que sirven como una barrera para la conectividad, tal como una autopista o un río. Las celdas que tienen valores de exclusión son ignoradas en los cálculos de conectividad y son escritas con valor de cero.
Ejercicios
8.1. Muestre las rejillas resultantes al aplicar las siguiente funciones focales a cada uno de las celdas de la rejilla que se muestra abajo (vecindario de 3x3 ):
- a. Rango
- b. Diversidad
- c. Máximo
- d. Mayoría
| 1 | 2 | 4 | |||
|---|---|---|---|---|---|
| 3 | 3 | ||||
| 1 | |||||
| 4 | 2 | 5 | |||
| 7 | 6 | ||||
| 9 | 8 |
8.2. Muestre las rejillas resultantes al aplicar los siguientes tipos de funciones de agrupamiento a la rejilla de entrada que se muestra más abajo:
- a. Agrupamiento solo ortogonal
- b. Agrupamiento ortogonal y diagonal
- c. Agrupamiento con distintos valores
- d. Agrupamiento con valores de exclusión (4=valor de exclusión)
| 1 | 2 | ||||
|---|---|---|---|---|---|
| 1 | 2 | ||||
| 2 | |||||
| 3 | 4 | 3 | |||
| 3 | 4 | 3 | |||
| 4 |