Análisis de entidades discretas ​

El objetivo de un SIG no solo es crear una base de datos de representaciones digitales de fenómenos geográficos, sino también proveer mecanismos para seleccionar, recuperar, y analizarlos.

Habiendo superado el problema de la recolección de datos y construir una base de datos geográfica, la próxima etapa consiste en cómo usar estos datos para proveer información que responda a preguntas sobre el mundo real.

El problema general del análisis de datos consta de una serie de aspectos:

• El usuario tiene un problema particular o consulta.

• La base de datos contiene información que puede ser usada para responder al problema del usuario y proveer dicha respuesta en la forma de un mapa, tabla o figura.

• Para responder la pregunta es necesario configurar un conjunto formal de operaciones de recuperación y análisis que extraigan los datos, calculen nueva información y desplieguen los resultados.

El tipo de técnica analítica que puede ser usada en datos geográficos depende grandemente del modelo de datos y la representación que ha sido utilizada. Es importante entender que diferentes modelos de datos y diferentes tipos de representación pueden requerir diferentes enfoques para que las consultas espaciales puedan ser formuladas.

La pregunta fundamental es si el modelo de datos básico se refiere a entidades en el espacio o a variaciones continuas de un atributo en el espacio. En el caso de las entidades, la recuperación y análisis de datos concierne a los atributos, localizaciones, y conectividad de las entidades y medidas de la forma en que ellas están distribuidas en el espacio; en el caso de superficies continuas, el análisis de datos concierne a la propiedades espaciales de la superficie.

Operaciones sobre atributos ​

Los atributos son propiedades de las entidades que definen lo que ellas son. Los atributos pueden ser divididos en tres tipos: aquellos que se refieren a la localización (p.ej. latitud, longitud, y/o elevación), aquellos que representan descriptores cuantitativos o cualitativos de alguna propiedad no geográfica (p.ej. parcela, propietario, tipo de terreno), y aquellos que son derivados de las propiedades geográficas de la entidad misma (p.ej. el área y perímetro).

Como en los sistemas de información tradicionales, nuevos atributos pueden ser agregados a las entidades como resultado de una operación de base de datos. Por ejemplo, un nuevo atributo puede ser calculado para parcelas de terreno mayores que un tamaño dado. Para el despliegue de información, el nuevo atributo puede utilizar color o un símbolo para representar este tipo de entidad en el mapa.

El nuevo atributo puede ser derivado por cualquier método de análisis lógico o matemático, incluyendo operaciones sobre las propiedades de proximidad y topología de las entidades. La recuperación sencilla de datos puede ser vista como la creación de un nuevo atributo temporal "seleccionado" cuando el conjunto de atributos asociados a la entidad coinciden con el criterio de búsqueda.

Recuperación mediante atributos ​

Las entidades pueden ser recuperadas o reclasificadas selectivamente, sobre sus atributos, mediante las reglas estándares del álgebra booleana que están incorporadas en los lenguajes de bases de datos tales como SQL.

El álgebra booleana usa los operadores lógicos AND, OR, XOR y NOT para determinar si una condición particular es cierta o falsa. Estos operadores pueden ser aplicados a todos los tipos de datos, sean ellos booleanos, nominales, ordinales, escalares, o direccionales.

Las operaciones booleanas no son solo aplicables a los atributos no espaciales de los elementos geográficos, ya que ellos también pueden ser aplicados a la localización y atributos geográficos derivados de las propiedades espaciales o topológicas de las entidades geográficas.

Por ejemplo, se pueden ejecutar consultas que involucren la forma de las áreas, o las propiedades de las fronteras de las áreas. En este caso, el resultado de la búsqueda podría tener un efecto en los patrones espaciales.

Operaciones topológicos ​

El sistema de geometría proporciona un conjunto de operadores que devuelven geometrías basadas en comparaciones lógicas entre conjuntos de puntos en una o más geometrías.

Buffer ​

La operación de buffer es utilizada para dibujar una zona alrededor de la entidad inicial, de forma que las fronteras de la zona o bufffer están todas a una distancia D desde las coordenadas de la entidad original. Si esta es una entidad puntual, entonces la zona es un círculo, si la entidad es una línea recta, un rectángulo con finales redondeados aparece, para una línea irregular aparece o un polígono aparece una figura poligonal.

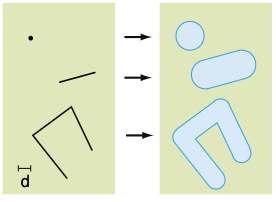
El buffer es en efecto un nuevo polígono que puede ser usado como una ayuda temporal para realizar consultas espaciales o agregarse por sí mismo a la base de datos.

Ejemplos típicos del uso de comandos de "buffering” con otras opciones de análisis son los siguientes:

• Determinar la cantidad de restaurantes de comidas rápidas dentro de 5km de la Casa Blanca
• Investigar el potencial de contaminación acuífera en términos de la proximidad de estaciones de gasolina a arroyos.
• Calcular el valor total de las casas que están incluidas dentro de 200 m de la ruta propuesta para una nueva carretera.
• Calcular la proporción de la población mundial que vive dentro de 100km del mar.
• Calcular la cantidad de pastos para ganado dentro de 5km de un pozo.

Convex Hull ​

Dada una geometría de entrada, el operador de cerco convexo (convex hull) devuelve una geometría que representa todos los puntos que están dentro de todas las líneas entre todos los puntos de la geometría de entrada.

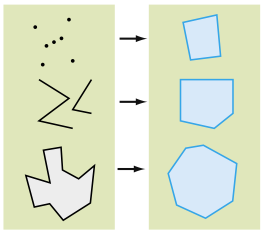
Un cerco convexo es el polígono más pequeño que envuelve a otra geometría sin ninguna zona cóncava.

Diferencia ​

El operador de diferencia devuelve una geometría que contiene puntos que están en la geometría base y resta puntos que están en la geometría de comparación.

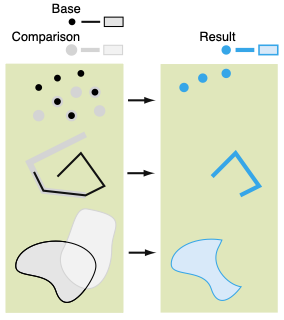
Esta operación es el equivalente del operador NOT en teoría de conjuntos.

Intersección ​

El operador intersección compara una geometría base (el objeto desde el que se llama al operador) con otra geometría de la misma dimensión y devuelve una geometría que contiene los puntos que están tanto en la geometría base como en la geometría de comparación.

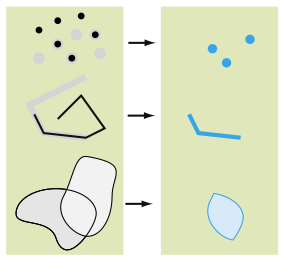
Esta operación es el equivalente de la operador AND en teoría de conjuntos.

Diferencia simétrica ​

El operador de diferencia simétrica compara una geometría base (el objeto desde el que se llama al operador) con otra geometría de la misma dimensión y devuelve una geometría que contiene los puntos que están en la geometría base o los puntos de la geometría de comparación, pero excluye los puntos de ambas geometrías.

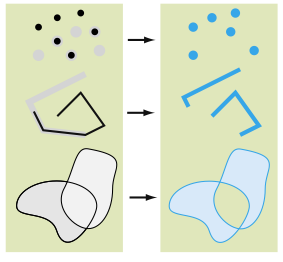
Esta operación es el equivalente de la operador XOR en teoría de conjuntos.

Unión ​

El operador de unión compara una geometría base (el objeto desde el que se llama al operador) con otra geometría de la misma dimensión y devuelve una geometría que contiene los puntos que están en la geometría base junto con los puntos de la geometría de comparación.

Esta operación es el equivalente de la operador OR en teoría de conjuntos. Los arcos de los elementos de entrada son separados en su intersección con los elementos de la capa de traslape. La tabla de atributos es actualizada y puede contener todos los atributos de las capas de entrada y de traslape. Sin embargo, generalmente solo se seleccionan algunos atributos para la capa de salida lo que incrementa el procesamiento significativamente.

Relaciones espaciales ​

El sistema de topológico incluye un conjunto de operadores booleanos que comprueban las relaciones espaciales entre una geometría base y una geometría de comparación. Estos operadores pueden aplicarse a puntos, multipuntos, polilíneas y polígonos.

La geometría base es el objeto que invoca el operador. La geometría de comparación es la geometría expresada como parámetro en el operador. El resultado del operador relacional se devuelve como un valor booleano. Con estos operadores no se crean nuevas geometrías.

Igualdad ​

Para que la geometría base y la geometría de comparación sean iguales, todos sus puntos constitutivos deben tener valores de coordenadas idénticos.

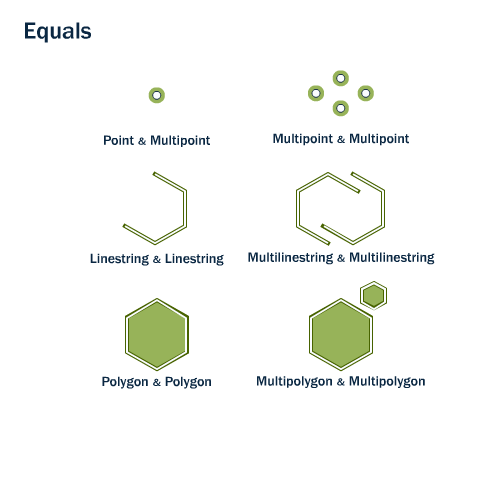
Las geometrías que se comparan deben tener la misma dimensión.

Dentro ​

Para que la geometría base esté dentro de la geometría de comparación, debe ser un subconjunto de esa geometría.

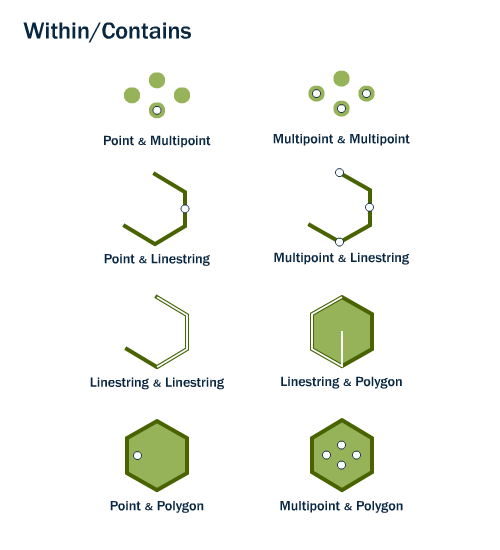
Una geometría no puede estar dentro de otra geometría de dimensión inferior.

Cruza ​

Para que la geometría base cruce una geometría de comparación, deben intersecarse en una geometría de menor dimensión que la de mayor dimensión.

Dos polilíneas se cruzan si su intersección contiene sólo puntos, y al menos uno de los puntos de intersección es interno a ambas polilíneas. Una polilínea y un polígono se cruzan si una parte conectada de la polilínea está en parte dentro y en parte fuera del polígono. Una polilínea y un polígono se cruzan si comparten una polilínea en común en el interior del polígono, que no es igual a toda la polilínea.

No es posible una relación de cruce entre un área base y un área de comparación. Esto se considera una relación de superposición.

Disjunta ​

Una geometría base es disjunta de una geometría de comparación si no comparten ningún punto.

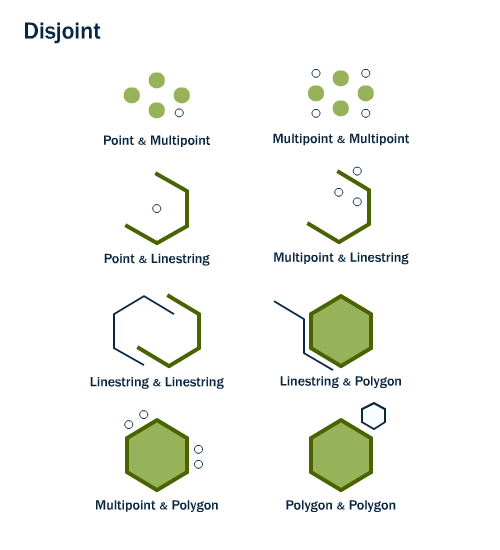
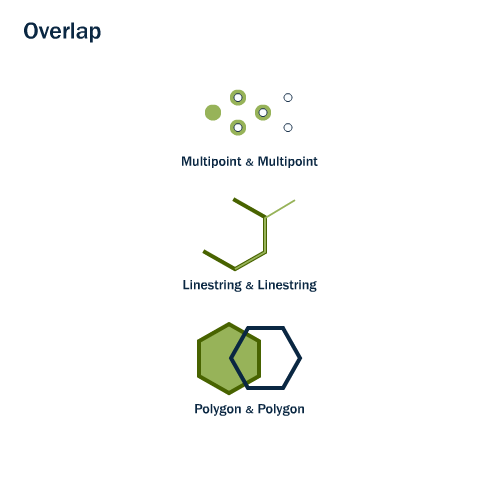
Traslape ​

Una geometría base se traslapa con una geometría de comparación si su intersección es una geometría de la misma dimensión. Una relación de solapamiento requiere que ambas geometrías sean de la misma dimensión.

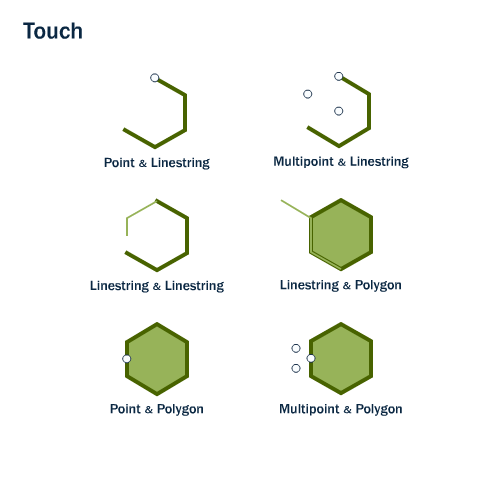
Toca ​

Dos geometrías se tocan cuando sólo se cruzan sus límites.

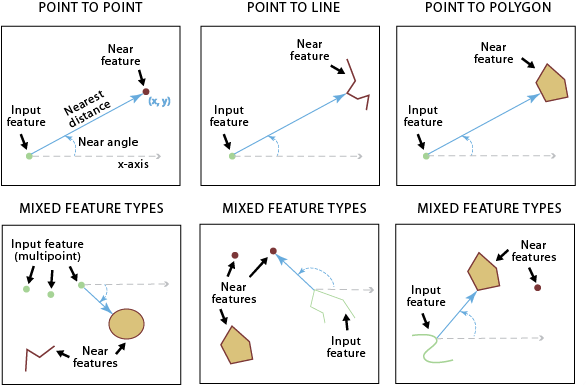
Operación de cercanía ​

Mediante la operación de cercanía es posible determinar los elementos más cercanos a otros elementos particulares. En este caso se requiere una capa de entrada y una capa de búsqueda. La capa de búsqueda incluye los elementos que son usados para calcular la distancia con cada elemento de la capa de entrada.

La cercanía puede ser calculada entre elementos puntuales, lineales o poligonales. La distancia se mide desde el vértice del elemento más cercano al otro elemento que se desea calcular.

Generalmente, este tipo de operación permite definir un rango de búsqueda máximo. La capa de salida contendrá los mismos elementos que la capa de entrada más algunos atributos adicionales que identifican el elemento más cercano y su distancia.

Ejercicios ​

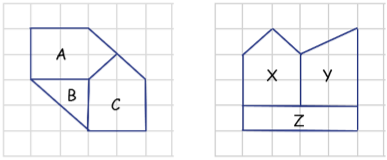
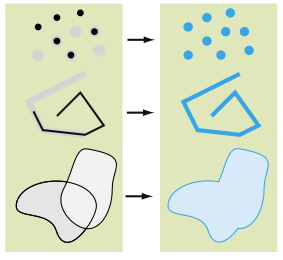
7.1. Muestre el resultado de ejecutar las siguientes operaciones de traslape de polígonos para las capas que se muestran abajo.

• a. Diferencia
• b. Intersección
• c. Diferencia simétrica
• d. Union