Métodos de acceso espacial ​

Con el fin de procesar eficientemente consultas espaciales se requiere especificar métodos de acceso, los cuales utilizan una estructura de datos llamada un índice. Estos métodos aceleran el acceso a los datos; es decir, reducen el conjunto de objetos a ser analizados cuando se procesa una consulta.

Utilización de métodos de acceso ​

Las consultas de puntos y de ventanas son ejemplos de consultas espaciales. En tales consultas, se buscan objetos cuya geometría contenga un punto o traslape un rectángulo. De no contar con un índice, estas operaciones requerirían una búsqueda secuencial y la posterior verificación de la condición espacial, mediante complicados algoritmos de geometría computacional.

Consultas espaciales ​

Rectángulo frontera mínimo ​

En lugar de indezar la geometría misma de los objetos, cuya forma puede ser compleja, se utiliza una aproximación a su geometría. La aproximación mas comúnmente utilizada es el rectángulo frontera mínimo, denotado por mbb (siglas en inglés). Esto reduce el costo de evaluar geometrías complicadas.

Indice espacial ​

Un índice espacial es construído como una colección de entradas. Cada entrada es de la forma [mbb,oid]. Aquí, oid identifica el objeto cuyo rectángulo frontera mínimo es mbb. Se supone que el oid permite accesar directamente el bloque de datos, en el archivo, que contiene la representación física del objeto.

Ejecución de la consulta espacial ​

La ejecución de una consulta espacial consiste de dos pasos:

• Filtrado: Se utiliza el índice espacial para seleccionar los objetos cuyos mbbs satisfacen la consulta. La salida es un conjunto de oids.
• Refinamiento: Utilizando algoritmos de geometría computacional se verifica la geometría real de los objetos filtrados en el primer paso.

Diseño de SAM ​

Para realizar el diseño de métodos de acceso espacial (SAM) se deben considerar estos hechos:

• El tamaño de la colección de objetos es mucho mas grande que el espacio disponible en memoria principal.
• El tiempo de acceso a disco es grande comparado con el acceso aleatorio en memoria principal.
• Los objetos son agrupados en bloques o páginas, que constituyen la unidad de transferencia entre memoria y disco.

Los SAM siguen alguno de estos enfoques:

• Estructuración del espacio: Estos se basan en particionar el espacio 2D en celdas rectangulares, independientemente de la distribución de objetos.
• Estructuración de los datos: Estos se basa en particionar el conjunto de objetos, y no el espacio circundante.

Métodos que estructuran el espacio ​

Dos tipos de familias de SAM son presentadas:

• El archivo de rejilla es una mejora de la rejilla fija diseñada para indezamiento de puntos.
• El quadtree lineal y el árbol de orden-z son ejemplos de estructuras de lineales.

Rejilla fija ​

El espacio de búsqueda es descompuesto en celdas rectangulares. La rejilla regular resultante es un arreglo de nxxny celdas de igual tamaño. Las celdas son asociadas con bloques en disco. Un punto es asignado a una celda si la celda contiene dicho punto. Los puntos asignados a una celda son almacenados secuencialmente en el bloque.

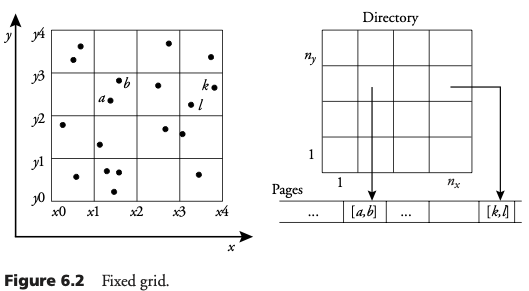
Sobreflujo en rejilla fija ​

La resolución de la rejilla depende del número N de puntos a ser indexados. Dado un bloque de capacidad M, se debe crear una rejilla de al menos N/M celdas. Cada celda contiene, en promedio, menos de M puntos. Si hay más de M puntos se produce sobreflujo. Los bloques de sobreflujo son encadenados a los bloques iniciales.

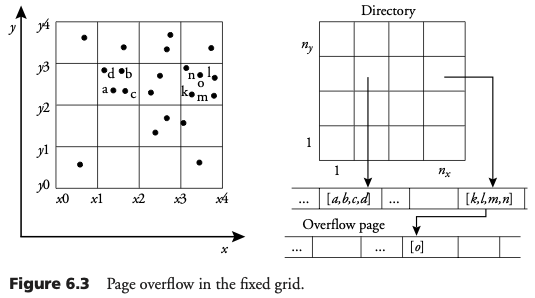
Archivo de rejilla ​

En un archivo de rejilla, al igual que en la rejilla fija, un bloque es asociado con cada celda. Cuando una celda provoca sobreflujo, ésta es dividida en dos celdas y los puntos son asignados a las nuevas celdas en donde caen.

A diferencia de la rejilla fija, en el archivo de rejilla las celdas son de diferente tamaño y la partición se adapta a la distribución de los puntos.

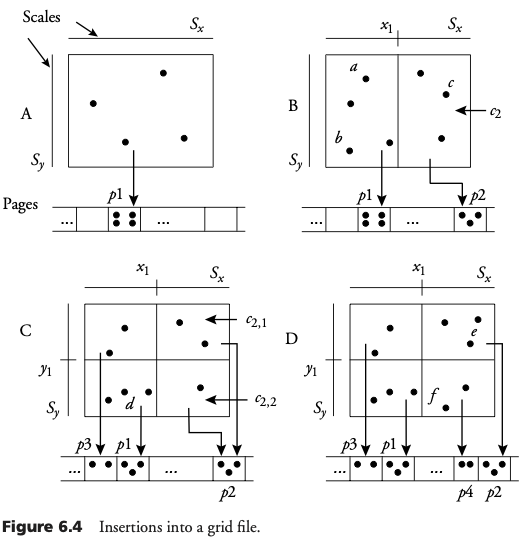
Indexamiento rectangular ​

Rejilla fija para indexamiento rectangular ​

La forma mas sencilla de asociar rectángulos a celdas es asignar los rectángulos a las celdas que los traslapan. Tres casos pueden suceder:

• El rectángulo contiene la celda
• El rectángulo intersecta la celda
• El rectángulo está contenido en la celda

En los dos primeros casos el rectángulo es asignado a múltiples celdas.

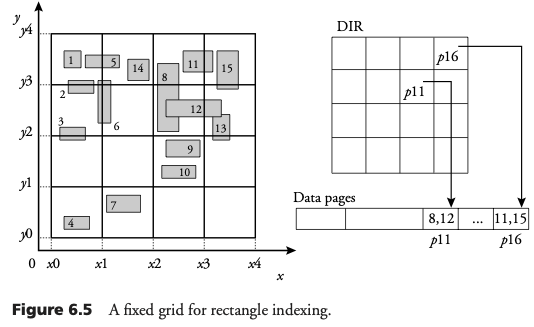
Archivo de rejilla para indexamiento rectangular ​

La inserción y borrado de objetos es similar al caso de puntos. Como consecuencia de la asignación a múltiples celdas, la división de celdas es más posible que ocurra.

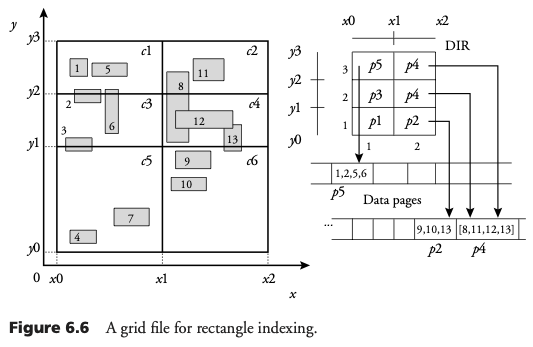
Inserción de rectángulo en archivo de rejilla ​

La inserción y borrado de objetos es similar al caso de puntos. Como consecuencia de la asignación a múltiples celdas, la división de celdas es más posible que ocurra.

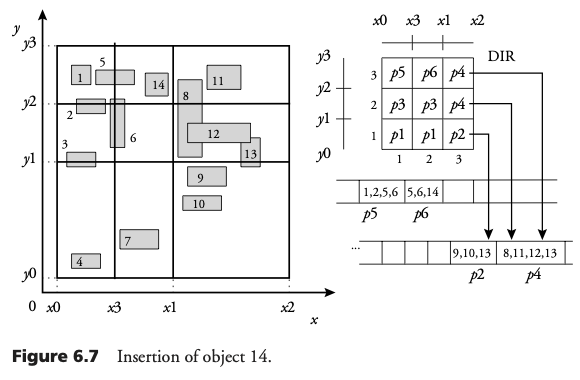
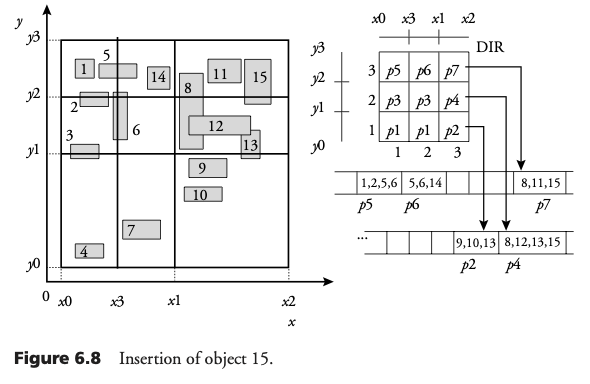
Consultas espaciales ​

Consultas de puntos ​

Dadas las coordenadas del punto se busca la celda que lo contiene. Luego se buscan los rectángulos que contienen el punto. Por último, se verifica la geometría verdadera del objeto.

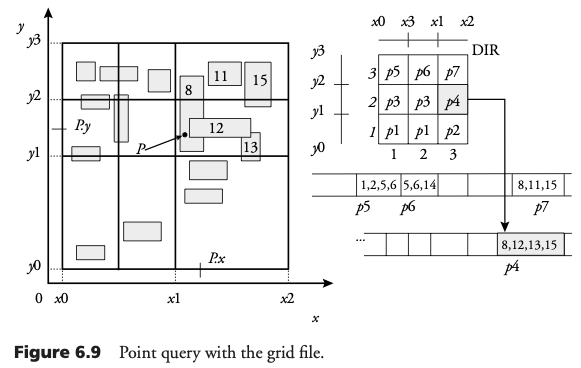
Consultas de ventana ​

Se buscan todas las celdas que traslapan la ventana. Luego se buscan los rectángulos que traslapan la ventana. Se eliminan rectángulos duplicados. Por último, se verifica la geometría verdadera del objeto.

Quadtree para rectángulos ​

El espacio de búsqueda es recursivamente descompuesto en cuadrantes. Esto se realiza hasta que el número de rectángulos traslape cada cuadrante en menos de la capacidad de un bloque. Los cuadrantes son nombrados Noroeste (NO), Noreste (NE), Suroeste (SO), y Sureste (SE). El índice es representado como un árbol cuaternario (cada nodo tiene cuatro hijos).

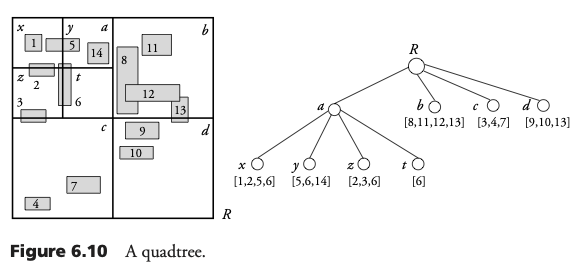
Consulta de punto en Quadtree ​

La consulta de punto es simple con un Quadtree. Se sigue un único camino desde la raíz hasta una hoja. En cada nivel, se elige entre los cuatro cuadrantes aquel que contenga el punto. La hoja es leída del archivo, y se realizan verificaciones posteriores contra la geometría real de los objetos.

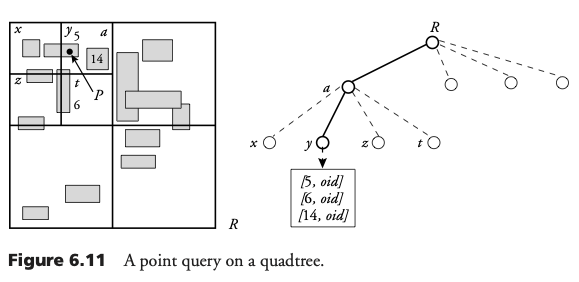
Inserción en Quadtree ​

Un rectángulo será insertado en cada hoja del cuadrante que traslape. Se deben seguir los caminos de todos aquellos hojas que traslapen el rectángulo. El bloque asociado con cada hoja debe ser leído. Pueden suceder dos casos:

• El bloque no está lleno: se agrega la entrada
• El bloque está lleno: El cuadrante es dividido en cuatro nuevos cuadrantes.

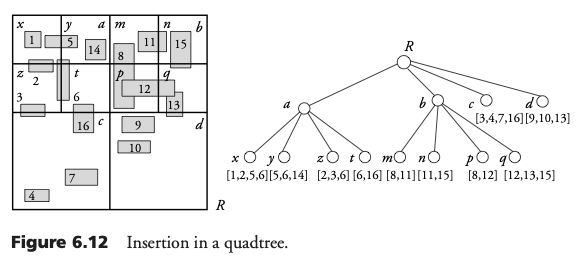
Curvas de relleno del espacio ​

Una curva de relleno del espacio define un orden total en las celdas de una rejilla 2D. Este orden es útil porque parcialmente preserva la proximidad. Dos métodos populares son:

• Curva de orden Z: NO, NE, SO, SE
• Curva de Hilbert: SO, NO, NE, SE

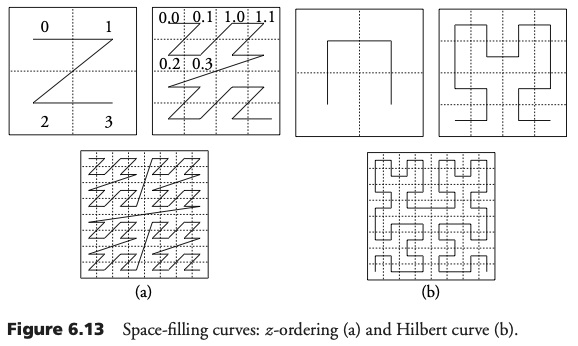
Etiquetado del Quadtree ​

Dado un quadtree de profundidad d. Cualquier hoja puede ser etiqueta con una hilera de tamaño <= d. El tamaño de la etiqueta es la profundidad de la hoja en el árbol

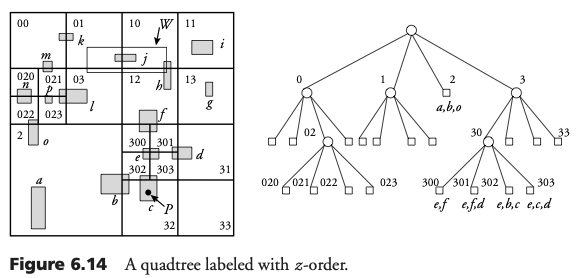
Métodos que estructuran los datos ​

Los SAMs de la familia de R-tree se adaptan a la distribución de los rectángulos en el plano. Al igual que el B-tree, éste forma una estructura jerárquica balanceada. Cada nodo del árbol es asignada a un bloque del disco. Cada nodo es asignado a un rectángulo, llamado el rectángulo directorio ( dr ).

El R-Tree original ​

Un R-Tree es un árbol balanceado con cada nodo asociado a un bloque de disco. Para todos los nodos del árbol (excepto la raíz), el número de entradas está entre m y M, donde 0 <= m <= M/2. Para cada entrada (dr, nodeid) en un nodo N no hoja, dr es el rectángulo directorio del nodo hijo de N, cuyo bloque es direccionado mediante nodeid. Para cada entrada de una hoja (mbb, oid), el mbb es el rectángulo frontera mínimo del componente del objeto almacenado en la dirección oid. La raíz tendrá al menos dos entradas, si no es hoja. Todas las hojas se encuentran en el mismo nivel.

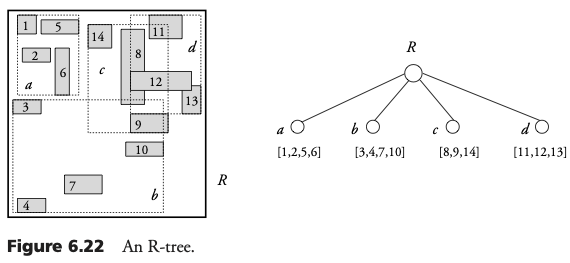
Búsqueda en un R-Tree ​

Primero se visitan todos los hijos de la raíz cuyo dr contenga el punto. Todos los sub-árboles con rectángulos que contengan el punto, deben ser visitados. El proceso es repetido en cada nivel del árbol hasta que las hojas son alcanzadas.

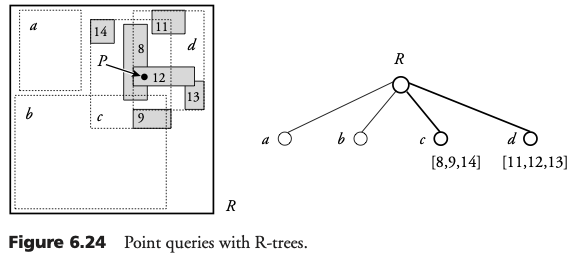
Inserción en R-Tree ​

Para insertar un objeto, el árbol es recorrido de arriba-hacia-abajo. En cada nivel, si se encuentra un dr que contiene el mbb del objeto entonces se analiza el sub-árbol correspondiente. Luego un nodo es elegido tal que contenga el mbb del objeto, o bien, la ampliación de su dr sea mínimo. Este proceso se repite hasta llegar a una hoja.

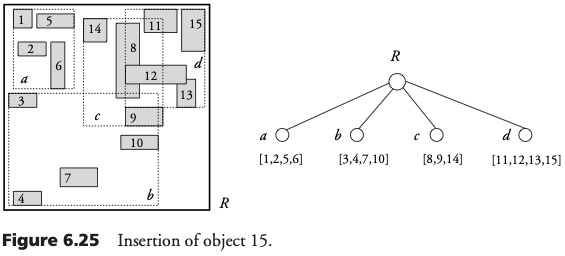
Si la hoja no está llena, una nueva entrada [mbb,oid] es agregada al bloque asociado con la hoja. Si el dr de la hoja tiene que ser ampliado, la correspondiente entrada en el nodo padre también debe ser actualizada. Este procedimiento se propaga hacia arriba hasta, posiblemente, llegar a la raíz.

Si la hoja está llena, ocurre una separación. Una nueva hoja es creada, y las entradas de la hoja original son distribuidas entre ambas. Se debe actualizar el correspondiente dr del nodo padre, y se debe agregar la nueva hoja en dicho nodo. Si el nodo padre también está lleno se produce una nueva separación en este nivel. Esto se propaga hacia arriba hasta, llegar a la raíz. En cuyo caso el árbol aumenta un nivel.

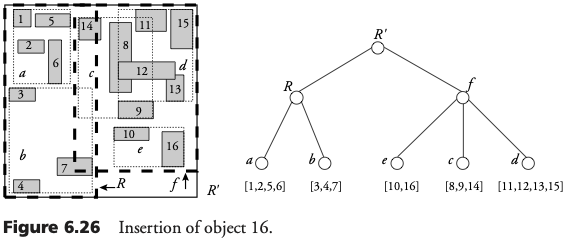
Estrategia de separación en R-Tree ​

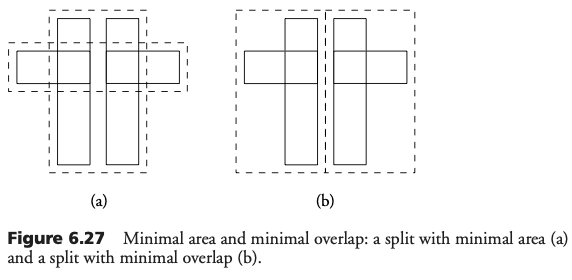
Existen muchas formas de realizar la separación de un nodo. Los requerimientos pueden ser:

• Minimizar el área total de los nodos
• Minimizar el traslape de los nodos

Estos dos requerimientos no son siempre compatibles.

El siguiente algoritmo trata de minimizar el área total de los nodos. Se seleccionan dos objetos semillas e y e' lo mas lejanos posibles. Entre ellos el espacio ”muerto” deber ser maximal. El espacio "muerto” se define como el área del mbb de e y e' menos la suma de las áreas de e y e'.

Cada uno de los restante objetos son insertados en el grupo mas cercano, es decir, aquel para el que la expansión es menor . La expansión del grupo es el espacio ”muerto” que resultaría al insertar el objeto en el grupo. Las dos partes del algoritmo ( inicialización de grupo e inserción de objetos) son cuadráticas.

Otro algoritmo selecciona los dos objetos semillas de forma que tengan la mayor distancia en un eje. Los objetos restantes son asignados al grupo cuyo mbb requiera menos ampliación. Este algoritmo es sencillo y lineal. Sin embargo, resultados experimentales muestran que presenta un importante traslape.

El R*Tree ​

En un R*Tree el algoritmo de separación busca separar los nodos en dos grupos mediante una línea imaginaria horizontal o vertical. Para elegir el eje (x ó y) se ordenan los rectángulos por su valor menor o mayor. Posteriormente, se calcula la suma S de perímetros. Por último, se elige el eje con suma S minimal. Dado el mejor eje, se elige la distribución con traslape mínimo. Si dos distribuciones comparten el mismo traslape mínimo, se elige el que tenga área mínima.

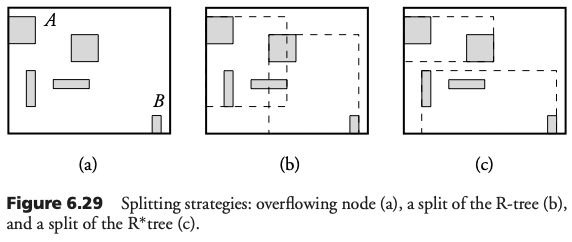
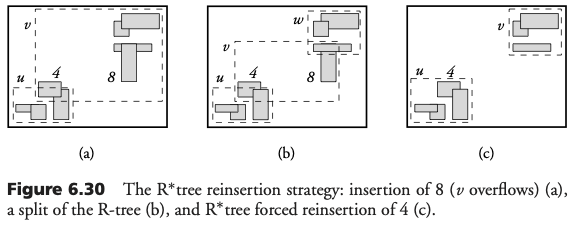
El R-Tree empacado ​

La versión estática de un R-Tree se le conoce como un R-Tree empacado. Si los rectángulos son conocidos a priori, se pueden ordenar y construir así el índice de abajo hacia arriba. Primero se llenan las hojas, luego los nodos del nivel más bajo, y así hasta construir la raíz. Se obtiene un B-Tree lleno hasta casi un 100%. Un problema es que al estar llenos los nodos en un 100%, cualquier inserción produce una separación.

Un algoritmo para empacar es el siguiente. Si se tienen N objetos, la cantidad mínima de hojas debe ser P = [N/M]. Se intenta crear un "tablero” de celdas, de forma que: filas * columnas = P. Se ordenan los objetos por la coordenada x de su centroide, luego se distribuyen en forma ordenada en tantos grupos como columnas tenga el ”tablero”.

Los objetos en cada grupo son ordenados por la coordenada y de su centroide, luego son distribuídos en forma ordenada en tantos grupos como filas tenga el "tablero”. Finalmente, se toman el conjunto de drs de las hojas, y se construye recursivamente los niveles superiores de acuerdo al mismo algoritmo.

El R+Tree ​

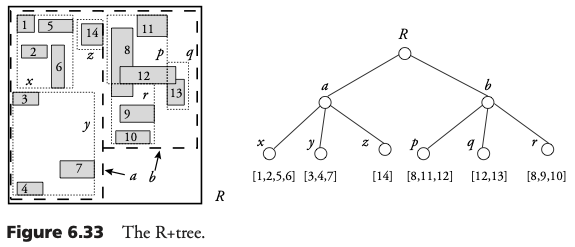
En un R+Tree, los drs en un nivel dado no se traslapan. La consecuencia de esto es que un consulta de punto es un camino único seguido desde la raíz hasta la hoja. El R+Tree se define de la siguiente forma: la raíz tiene al menos dos entrados, excepto cuando es una hoja, y los dr de dos nodos en el mismo nivel no se traslapan.

Si el nodo N no es una hoja, su dr contiene todos los rectángulos en el sub-árbol cuya raíz es N. Un rectángulo de una colección a ser indexado es asignado a todas los nodo hoja.

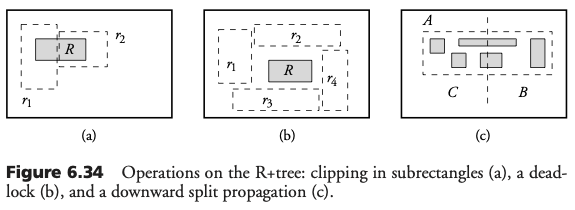
Operaciones en el R+Tree ​

La construcción y mantenimiento del R+Tree es mas compleja que con el R-Tree. Cuando un rectángulo traslapa los drs de más de un nodo, éste debe ser recortado y sus partes insertadas en cada nodo (duplicación). Bajo ciertas situaciones no es posible agregar un objeto sin provocar traslape. Cuando un nodo se llena, éste debe ser separado y la actualización debe ser propagada hacia arriba.

Referencia ​

• Tomado del capítulo 6 del libro "Spatial Databases with Applications to GIS" de Philippe Rigaux, Michel Scholl y Agnes Voisard.

Ejercicios ​

1. Muestre la división espacial resultante al incorporar los siguientes datos puntuales, utilizando los métodos de acceso espacial que se señalan más abajo: a = (3,4), b = (6,7), c = (8,3), d = (3,6), e = (4,3), f=(6,6), g=(3,3), h=(8,9), i = (4,7) y j = (2,8). Considere que cada bloque de datos cuenta únicamente con capacidad para dos puntos. Utilice un área con límite inferior en (0,0) y superior en (10,10).

• Rejilla fija de 4x4
• Archivo de rejilla (iniciando con división en el eje x)
• Quadtree

2. Muestre la división espacial (y el árbol) resultante al incorporar los siguientes rectángulos frontera (bounding box), utilizando los métodos de acceso espacial que se señalan más abajo: a = (1,8,2,9), b = (7,6,9,7), c = (1,1,2,5), d = (3,2,5,3), e = (7,8,8,10), f=(1,6,3,7), g=(4,7,5,9), y h=(6,3,8,2). En todos los casos el orden de las coordenadas es (x mínimo, y mínimo, x máximo, y máximo). Considere que cada bloque de datos cuenta únicamente con capacidad para dos objetos o rectángulos. Utilice un área con límite inferior en (0,0) y superior en (10,10). Dibuje el dr (rectángulo directorio) de cada nodo del árbol.

• R Tree original (intente minimizar el espacio muerto)
• R* Tree (intente alternar división horizontal/vertical)
• R+Tree